JKTuring 1.0

Was sind Turing Maschinen?
Beschreibung der Software
Eingabekonventionen für Turing-Programme
Links
Download & Installation

Was sind Turing Maschinen?

Das Programm JKTuring 1.0 implementiert eine Turing-Maschine auf einem PC (MS Windows).

Alan Turing führte diese nach ihm benannten Maschien 1936 zum theoretischen Studium der Berechenbarkeit ein. Eine Turing-Maschine arbeitet auf einem einseitig unendlichen Band, das in unendlich viele Zellen a_n (n = 0, 1, 2, ...) aufgeteilt ist, die jeweils ein Wort aus dem verwendeten Alphabet E (z.B. E={1, 0} oder E={0, 1, X, Y} usw.) enthalten können. Die Maschine beginnt am Anfang des Bandes (Tape) mit ihrer Arbeit (a₀). Die Maschine selber ist in einen festen ("Hardware") und einen variablen Teil ("Software" bzw. "Programm") aufgeteilt. Die Turing-Maschinen beschreiben also eigentlich eine ganze Klasse von Maschinen (unendlich viele!), weil das Programm, das nach bestimmten Regeln aufgebaut sein muss, unendlich lang und komplex sein kann. Den Aufbau einer Turing-Maschine zeigt die folgende Abbildung:

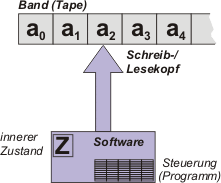
Die Maschine befindet sich zu jedem Zeitpunkt in einem definierten inneren Zustand Z. Zu Anfang ist dies der Startzustand Z^*, der im Programm festgelegt wird. Sobald die Maschine mit ihrer Arbeit fertig geworden ist, befindet sie sich im Endzustand Z^#, der ebenfalls im Programm definiert wird. Sie hört dann auf mit der Arbeit.

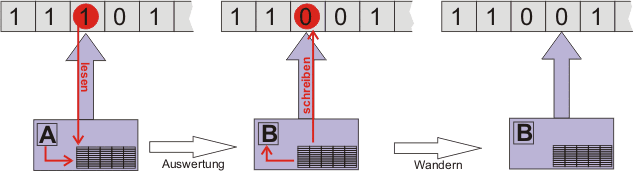
Ein Turing Maschine hat einen Schreib-/Lesekopf als einzige Hardware, der immer genau auf eine Zelle des Bandes a_m zeigt. Er stellt am Anfang eines Zykluses den Wert der Zelle unter ihm zur Verfügung und schreibt nach der Auswertung das Ergebnis an die selbe Stelle a_m des Bandes. Danach wandert er je nach Anweisung im Programm um eine Position nach rechts oder links. Zum Schluss geht die Maschine noch in einen neuen internen Zustand über.

Im Programm wird je nach innerem Zustand Z und gelesenem Wert a_m entschieden, was geschrieben werden soll und in welche Richtung sich der Schreib-/Lesekopf bewegen soll. Dabei muss immer etwas geschrieben werden und der Kopf muss sich immer bewegen (er kann also nicht stehen bleiben). Somit kann man ein Programm für eine Turing-Maschine als Tabelle schreiben, bei der jede Zeile genau einer Kombination von internem Zustand und gelesenem Wert entspricht. Der Ablauf eines solchen Zykluses wird in der folgenden Graphik leicht verständlich:

Hier ein beispiel für ein kleines Turing-Maschinen-Programm:

Zustand	Eingabe	Operation (Ausgabe, Verschiebung)	Folgezustand	Bemerkung
A	1	0,rechts	A	Anfangszustand Z^*
	0	0,rechts	B
B				Endzustand Z^#

Das Programm lässt sich auch als Graph darstellen und wird so leichter verständlich:

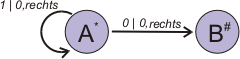
Das Programm besagt folgendes:

Zustand A ist der Anfangszustand der Maschine. Mit ihm beginnt die Ausführung.
Wenn sich die Maschine im Zustand A befindet und unter dem Schreib/Lesekopf eine "1" steht, dann schreibe eine "0" und gehe nach rechts. Bleibe im Zustand A.
Wenn sich die Maschine im Zustand A befindet und unter dem Schreib/Lesekopf eine "0" steht, dann schreibe eine "0" und gehe nach rechts. Gehe in den Zustand B (Endzustand) über.
Zustand B ist der Endzustand der Maschine und beendet die Ausführung.

Das Start-Tape zu diesem Programm könnte so aussehen:

0 ....

Auf diesem Tape würde das Programm alle "1" durch "0" ersetzen und bei der ersten "0" in den Endzustand übergehen und sich beenden.

Es gibt aber auch wesentlich komplexere Programme. Im Software-Paket JKTuring 1.0 ist etwa eines enthalten, dass eine "1"-Kette verdoppeln kann. Dies entspricht bei grundlegender Betrachtung der Mathematischen Rechenopertaion *2, wenn man Zahlen als ihrem Wert entsprechende Reihen von "1" darstellt.

Wie wir gesehen haben kann also eine Turing-Maschine von ganz einfachen Grundoperationen ausgehend, mit einem endlichen Programm viele Probleme lösen. Man muss das Problem nur in eine für die Maschine verständliche Form bringen und das Ergebnis der Maschine interpretieren können.

Wie JKTuring 1.0 zeigt ist es möglich eine Turing-Maschine auf dem PC zu simulieren. Viel beeindruckender ist jedoch, dass das umgekehrte ebenfalls möglich ist: Wenn das Programm nur genügend Koplex wird (es bleibt dabei aber immer noch endlich) kann man ohne weiteres einen PC auf einer Turing-Maschine simulieren! Dies besagt die sog. Church'sche These: Alles was man für intuitiv berechendbar hält kann man mit einer Turing-Maschine ausrechnen.

Intuitiv berechenbar heißt dabei, dass für ein Problem ein Lösungs-Algorithmus angegeben werden kann.

Beschreibung der Software:

Das Programm und der Anfangszustand des Tapes werden als Text in JKTuring eingegeben. Danach kann man die Maschine ihr Werk verrichten lassen. Über die rechte Maustaste können sowohl Programm, als auch Tape gespeichert und geladen werden.

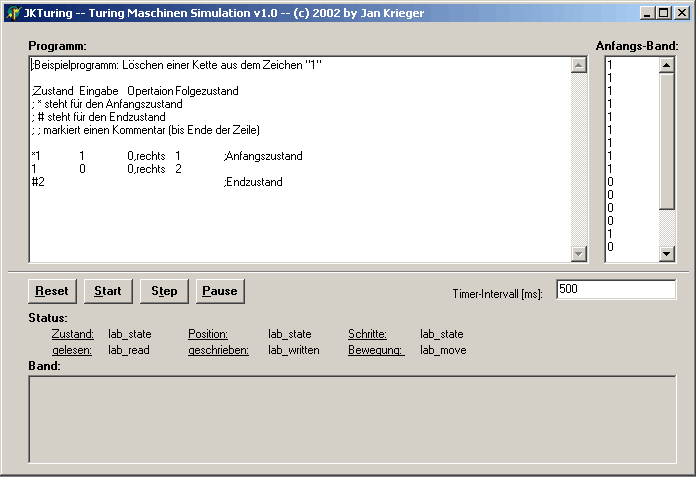
Im unteren Teil des Fenster gibt es vier Buttons für die Bedienung der Programms und ein Eingabefeld, in das man ein Zeit-Intervall (in Millisekunden) eingeben kann, das zwischen zwei Zyklen der Maschine liegt.

Der aktuelle Zustand von Band und maschine wird ganz unten angezeigt.

Die Buttons haben folgende Bedeutung:

Reset: Setz die turing Maschine in den Ausgangszustand zurück und unterbricht die Ausführung.
Start: Startet die Turing-Maschine an Position 0 und im Startzustand. Die Zyklen werden automatisch ausgeführt.
Step: Führt einen einzelnen Zyklus aus.
Pause/Go on: Hält die Turing-Maschine an bzw. lässt sie weiterlaufen.

Eingabekonventionen für Programme:

Turing-Programme werden ähnlich wie in der Tabelle dargestellt eingegeben. Eine Tabellen-Zeile (also eine Kombination aus Zustand und gelesenem Wert) belegt genau eine Zeile des Programms. Die einzelnen Spalten werden dabei durch Tab-Stops getrennt. Es ist möglich Kommentare einzufügen. Diese beginnen immer mit dem Zeichen ";" und gehen bis ans Ende der aktuellen Zeile.

Ein Programm sieht folgendermaßen aus:

Zuerst wird der innere Zustand angegeben. Danach folgt (hinter einem Tab) die Eingabe. Nach einem weiteren Tab steht (durch "," -> Komma) getrennt die Ausgabe und die Richtung, in die sich der Kopf bewegen soll. Nach einem weiteren Tab folgt dann der Endzustand, in den übergegangen werden soll.
Kommentare dürfen ganze Zeilen belegen, oder hinter einer Befehlssequenz stehen.
Der Anfangszustand wird durch einen "*" (Asterisk/Stern) vor dem Zustandsbezeichner markiert.
Der Endzustand wird durch ein "#" (Doppelkreuz) vor dem Zustandbezeichner markiert. Er muss hinter dem Zustandsbezeichner keine weiteren daten enthalten (wie Eingabe, Ausgabe ...).
Der Bezeichner für einen Zustand und das Alphabet, das die Maschine benutzt dürfen aus beliebigen ASCII-Zeichen(folgen) bestehen. Nur die Zeichen ";", "#", "*" und der Tabulator dürfen nicht vorkommen.

Damit sieht das Programm zu obigem Beispiel wie folgt aus:

;Beispielprogramm: Löschen einer Kette aus dem Zeichen "1"

*1    1    0,rechts    1    ;Anfangszustand
1     0    0,rechts    2 
#2                          ;Endzustand

Links

Die Turing-Maschine
Turing-Maschine: "Auf dieser Seite möchte ich die Originalarbeit zu dem von Alan M. Turing veröffentlichten Berechenbarkeitsformalismus, der später als Turing-Maschine bezeichnet wurde, vorstellen. Die Arbeit mit dem Titel On computable numbers, with an application to the Entscheidungsproblem erschien 1937 in Proceedings of the London Mathematical Society (2) 42. Für eine kürzere und vielleicht auch einfachere Einführung zu dem Begriff der Turing-Maschine möchte ich auf die vielen Seiten im WWW verweisen, die sich mit diesem Thema beschäftigen"
Turing-Maschine Simulator: eine Turing-Maschine in JAVA
turing.htm: Turingmaschine und Halteproblem
Demonstration einer Turing Maschine
Alan M. Turing - Turing-Maschine (1)

Download & Installation

Sie können die WIndows-Software JKTuring als ZIP-Archiv herunterladen. Sie enthält diese Dokumentation und einige Beispiel-programm, sowie zugehörige Tapes. Das ZIP-Archiv jkturing.zip ist 270 kB groß und kann mit WinZIP oder Powerarchiver oä. entpackt werden. Alle dateien sollten in ein verzeichnis kopiert werden. Von dort aus kann man dann die Datei jkturing.exe starten. Sie ist das eigentliche Programm. Die Dokumentation befindet sich im Unterverzeichnis .\doku\jkturing.html