BZR - 3.2 Rechenmodelle für die zeitliche Reaktion

Inhalt --

3 Mathematische modelle und Simulation -- 3.2.2 FKN-Modell

3.2 Rechenmodelle für die zeitliche Reaktion

3.2.1 Der ,,Brüsselator``

Der sog. Brüsselator (Der Brüsselator wurde von I. Prigogine und R. Lefever an der Université Libre de Bruxelles in Belgien entwickelt, daher der Name) ist ein recht einfaches Modell für oszillierende Systeme, das zwei oszillierende Variablen enthält. Er ist nicht direkt auf die BZR übertragbar, liefert aber ähnliche Ergebnisse und ist gut dazu geeignet, die grundlegenden Techniken der Simulation zu erklären. Das Modell basiert auf den folgenden ,,Reaktionsgleichungen``: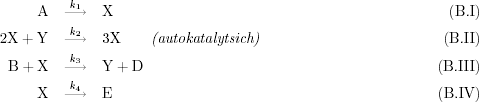

Hierbei sind k₁ .. k₄ Geschwindigkeitskonstanten für die Reaktionen (B.I)...(B.IV). Aus diesen Gleichungen ergibt sich die Summengleichung:

Dieses Modell wurde schon bei seiner Vorstellung 1967 [Prigogine, Lefever 1968] als physikalisch unrealistisch bezeichnet, weil der trimolekulare Schritt (B.II) in der Natur nicht denkbar ist. Man kann aus (B.V) leicht ersehen, dass X und Y hier als Katalysatoren fungieren, da sie sich in der Summengleichung herauskürzen. Es handelt sich hier um ein Fließgleichgewicht, weil während der Berechnung die Stoffmengen von A und B konstant gehalten werden und die Produkte D und E keine Rückwirkung auf das System haben.

Aus diesem Modell erhält man leicht Terme, die die Geschwindigkeit angeben, mit denen die Reaktionen abläuft:

$\begin{displaymath}v_1 = k_1 \cdot A;\qquad v_2 = k_2 \cdot X^2Y;\qquad v_3 = k_3 \cdot BX;\qquad v_4 = k_4 \cdot X;\end{displaymath}$

Daraus ergeben sich die kinetischen Gleichungen für die Stoffmengenumsätze $\frac{dx}{dt}$ und $\frac{dy}{dt}$ durch Addieren und Subtrahieren:

$\begin{displaymath}\frac{dx}{dt} = 1\cdot v_1 + (-2+3)\cdot v_2 - 1\cdot v_3 - 1\cdot v_4 = k_1A + k_2X^2Y - k_3BX - k_4X\end{displaymath}$	(B.6)
$\begin{displaymath}\frac{dy}{dt} = 1\cdot v_3 - 1\cdot v_2 = k_3BX - k_2X^2Y\end{displaymath}$	(B.7)

Dies bedeutet für $\frac{dx}{dt}$ , dass mit der Geschwindigkeit v₁ und v₂ je ein X gebildet, aber auch mit v₃ und v₄ je eines verbraucht wird. Bei (B.II) werden eigentlich 3 X gebildet, aber es werden auch zwei davon wieder verbraucht, was zu einem gesamten Zugewinn von 1 X führt. Das Zustandekommen von $\frac{dy}{dt}$ lässt sich analog erklären [Prigogine, Lefever 1968, Franck 1978, Kondepudi, Prigogine 1998].

Dieses DGS habe ich in ein Computerprogramm umgesetzt. Hierbei verwende ich die Lösungsmethode, die ich in 3.1 angedeutet habe. Das Programm hat folgenden Aufbau (abgefasst in einer algorithmische Pseudosprache, wie sie in einigen Artikeln in der Zeitschrift ,,Spektrum der Wissenschaft`` verwendet wird [Dewdney 1992b]):

1 X <-- X₀
2 Y <-- Y₀
3 A <-- A₀
4 B <-- B₀
5 wiederhole
6    n_x <-- k₁·A + k₂·X²·Y - k₃·B·X - k₄·X
7    n_y <-- k₃·B·X - k₂·X²·Y
8    X <-- X + n_x·t
9    Y <-- Y + n_y·t
10   zeichne X und Y
11 Ende wiederhole

In den Zeilen (Z.) 1-4 werden den Variablen die Startbedingungen zugewiesen. Danach beginnt die Iteration durch eine Schleife (Z. 5-11), die laufend wiederholt wird: zuerst werden die Stoffmengenänderungen pro Zeiteinheit $n_x=\frac{dx}{dt}$ und $n_y=\frac{dy}{dt}$ mit den oben genannten Formeln (B.6) und (B.7) berechnet (Z. 6, 7). Danach werden diese Änderungen mit dem Zeitintervall dt multipliziert, um die Zeit aus dem Nenner zu kürzen. Es bleiben dann nur die Stoffmengenänderungen dx und Y während der Zeit t stehen, die zu den alten X- und Y-Werten addiert werden (Z. 8, 9). Je nachdem, ob n_x bzw. n_y positiv oder negativ sind, erniedrigt oder erhöht sich dann die Stoffmenge von X und Y. Danach werden die Werte auf dem Bildschirm ausgegeben (Z. 10). Wenn die Schleife das nächste Mal durchlaufen wird, sind die eben berechneten Werte die alten und werden in die Rechnung eingesetzt.

Ich habe das gerade beschriebene Programm in der Programmiersprache Borland Delphi 5 (Objekt-Pascal für Windows, siehe Borland Homepage) umgesetzt. Es gibt folgende Graphen für den Brüsselator aus:

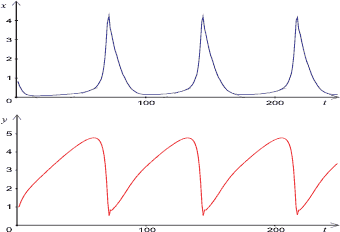
Abb.:Funktionsgraphen des Brüsselator-Modells mit den in [Kondepudi, Prigogine 1998] angegebenen Paramtern: A₀=1; B₀=3; X₀=1; Y₀=1; k₁=k₂=k₃=k₄=1 und dt=0,01. Blaue Kurve: X; Rote Kurve: Y. Zeitachse in Rechenschritten.

Eine eingehender Vergleich aller Rechenmodelle mit den Versuchsergebnissen erfolgt in Abschnitt 3.2.4. Das beschriebene Programm befindet sich zusammen mit den Programmen für die folgenden Rechenmodelle auf der beigelegten CD-ROM. Die Bedienung wird in Anhang B beschrieben.

Inhalt --

3 Mathematische modelle und Simulation -- 3.2.2 FKN-Modell

druckbare Version